|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fractali > curbe > curba dragonului
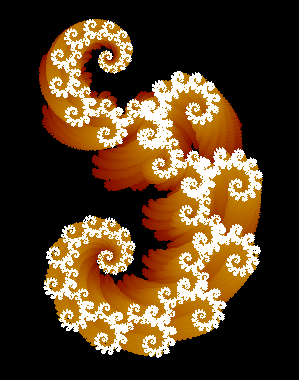
Se traseaza (incepe) cu un segement de dreapta. La prima iteratie, se inlocuieste acest segment cu alte doua segmente, fiecare scalate cu ratia r=
in asa fel incat segmantul original sa fie ipotenuza unui triunghi isoscel. De-alungul segmentului original trasam (punem) cele doua segmente noi spre stanga. La a doua iteratie, inlocuim fiecare dintre segmente cu doua noi segmente la unghi drept, fiecare scalate cu ratia r. Noile segmente sunt asezate la stanga apoi la dreapta de-alungul segmentelor primei iteratii. Se continua aceasta constructie, alternand mereu segmentele noi intre stanga si dreapta de-alungul segmentelor interatiei anterioare. Acesata constructie genereaza "Curba Dragonului". Figura ce urmeaza arata primele trei iteratii pentru constructia curbei.
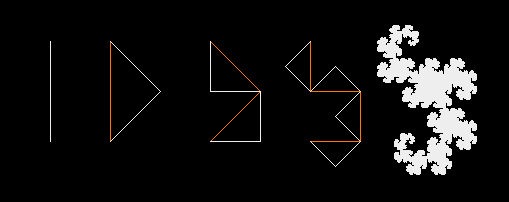
Aici este aratat cum a fost construit dragonul original de Heighway. Se impatureste o foaie de carton in patru. Se impatureste din nou in aceeasi directie. Se continua mereu in aceeasi directie impaturirea. Dupa cateva impaturiri, se deschide bucata de carton astfel incat fiecare impaturire sa fie un unghi drept si se priveste hartia de pe margine. In general, n impaturiri dau ordinul al n-lea al dragonului. Figura ce urmeaza are ordinul al-3 lea (in partea de jos) si ordinul al-4 lea (in partea de sus) construit dintr-o bucata ingusta de carton
Inca o metoda de a construi dragonul Heighway, incepe cu un triunghi isoscel spre dreapta. H0. Inlocuim acest triunghi cu doua triunghi isoscele spre dreapta astfel incat ipotenuzele triunghiurilor noi sa fie asezate de parti egale ale triunghiului vechi. Lucrand in jurul lui H0, incepand din partea stanga, punem noul triunghi astfel incat sa arate inafara triunghiului vechi si celalat triunghi nou sa arate inspre interiorul triunghiului vechi pentru a obtine H1. Pentru urmatorul pas, repetam procesul pentru fiecare dintre triunghiurile care compun H1, de data asta plsand triunghiurile noi astfel incat ele sa arate Inafara, Interior, Interior, Inafara, asa cum e aratat in figura urmatoare. Acest model Inafara, Interior, Interior, Inafara e repetat pentru fiecare din iteratiile care urmeaza in constructia dragonului.
Dragonul Heighway este setul limitat de astfel de iteratii. Liniile de dreapta ce compun ipotenuzele triunghiurilor formeaza aceeasi cale ca si constructia descrisa mai sus. Pentru a ne gandi la aceasta constructie ca fiind rezultatul unor transformari rafinate consideram prima iteratie a segmentului de dreapta de la (0,0) pana la (1,0) asa cum e aratat in figura ce urmeaza prin cele doua linii rosii.
Generarea
Daca se modifica unghiurile dintre segmente atunci se creeaza o noua familie de dragoni,mutanti,cum este cel din figura ce urmeaza.
Exemplu FLASH